[DP] 백준 2240번 자두나무
https://www.acmicpc.net/problem/2240
2240번: 자두나무
자두는 자두를 좋아한다. 그래서 집에 자두나무를 심어두고, 여기서 열리는 자두를 먹고는 한다. 하지만 자두는 키가 작아서 자두를 따먹지는 못하고, 자두가 떨어질 때까지 기다린 다음에 떨어
www.acmicpc.net
무식한 방법(완전탐색) 으로 제출 했더니 시간초과..
이 문제는 DP 문제라고한다. 근데 도대체 어느 부분에 메모이제이션을 적용할 수 있는거지?
여러 블로그 글들을 봐도 이해가 잘 안됐지만, 나는 아래 아이디어를 시작으로 점점 해답에 가까워지는게 느껴졌다.
짝수번 (0, 2, 4, 6...) 움직였다면 >>> 위치는 무조건 1
홀수번 (1, 3, 5, 7...) 움직였다면 >>> 위치는 무조건 2
즉, 움직인 횟수를 알면, 어느 시간에 있던 현재 위치를 쉽게 알 수 있다.
DP배열을 [시간][위치][움직인횟수] 와 같이 3차원으로 생각해볼수도 있지만, 움직인 횟수를 알면 현재 위치도 계산할 수 있기 때문에 [시간][움직인횟수] 면 충분한듯.
그래서 DP 배열을 [시간][움직인 횟수] 로 정함.
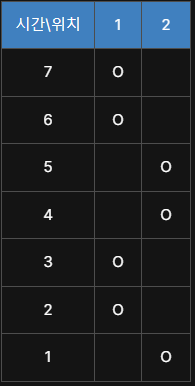
시간에 따른 자두의 위치를 표로 나타내면 위 표와 같음.
이때, 가장 마지막 초(7초) 부터 1초 까지, 역순으로, 최대로 잡을 수 있는 자두의 갯수를 표로 나타내면 다음과 같다.
아래 표를 그릴 수 있으면, 이 문제는 이해가 끝났다고 생각한다.

문제에 있는 예를 입력해보면, 로그가 아래와 같이 찍힌다.
위 표에서의 잡은 갯수와 아래 로그("CatchCnt") 의 값이 일치한다.
7 2
2
1
1
2
2
1
1
#01 time, moveCnt = (1, 1)
#01 time, moveCnt = (2, 2)
#01 time, moveCnt = (3, 2)
#01 time, moveCnt = (4, 2)
#01 time, moveCnt = (5, 2)
#01 time, moveCnt = (6, 2)
#01 time, moveCnt = (7, 2)
#02 time, moveCnt = (7, 2), CatchCnt = 1
#02 time, moveCnt = (6, 2), CatchCnt = 2
#02 time, moveCnt = (5, 2), CatchCnt = 2
#02 time, moveCnt = (4, 2), CatchCnt = 2
#02 time, moveCnt = (3, 2), CatchCnt = 3
#02 time, moveCnt = (2, 2), CatchCnt = 4
#01 time, moveCnt = (2, 1)
#01 time, moveCnt = (3, 2)
#03 time, moveCnt = (3, 2), CatchCnt = 3
#01 time, moveCnt = (3, 1)
#01 time, moveCnt = (4, 2)
#03 time, moveCnt = (4, 2), CatchCnt = 2
#01 time, moveCnt = (4, 1)
#01 time, moveCnt = (5, 2)
#03 time, moveCnt = (5, 2), CatchCnt = 2
#01 time, moveCnt = (5, 1)
#01 time, moveCnt = (6, 2)
#03 time, moveCnt = (6, 2), CatchCnt = 2
#01 time, moveCnt = (6, 1)
#01 time, moveCnt = (7, 2)
#03 time, moveCnt = (7, 2), CatchCnt = 1
#01 time, moveCnt = (7, 1)
#02 time, moveCnt = (7, 1), CatchCnt = 0
#02 time, moveCnt = (6, 1), CatchCnt = 1
#02 time, moveCnt = (5, 1), CatchCnt = 3
#02 time, moveCnt = (4, 1), CatchCnt = 4
#02 time, moveCnt = (3, 1), CatchCnt = 4
#02 time, moveCnt = (2, 1), CatchCnt = 4
#02 time, moveCnt = (1, 1), CatchCnt = 5
#01 time, moveCnt = (1, 0)
#01 time, moveCnt = (2, 1)
#03 time, moveCnt = (2, 1), CatchCnt = 4
#01 time, moveCnt = (2, 0)
#01 time, moveCnt = (3, 1)
#03 time, moveCnt = (3, 1), CatchCnt = 4
#01 time, moveCnt = (3, 0)
#01 time, moveCnt = (4, 1)
#03 time, moveCnt = (4, 1), CatchCnt = 4
#01 time, moveCnt = (4, 0)
#01 time, moveCnt = (5, 1)
#03 time, moveCnt = (5, 1), CatchCnt = 3
#01 time, moveCnt = (5, 0)
#01 time, moveCnt = (6, 1)
#03 time, moveCnt = (6, 1), CatchCnt = 1
#01 time, moveCnt = (6, 0)
#01 time, moveCnt = (7, 1)
#03 time, moveCnt = (7, 1), CatchCnt = 0
#01 time, moveCnt = (7, 0)
#02 time, moveCnt = (7, 0), CatchCnt = 1
#02 time, moveCnt = (6, 0), CatchCnt = 2
#02 time, moveCnt = (5, 0), CatchCnt = 2
#02 time, moveCnt = (4, 0), CatchCnt = 3
#02 time, moveCnt = (3, 0), CatchCnt = 5
#02 time, moveCnt = (2, 0), CatchCnt = 6
#02 time, moveCnt = (1, 0), CatchCnt = 6
6
하이라이트된 부분은, 이전에 계산한 값을 바로 리턴 한 부분.
위 표에서의 잡은 갯수와 아래 로그("CatchCnt") 의 값이 일치한다.
위 표와 같은 결과가 나오도록 코딩하면 다음과 같다.

로그를 제거한 버전은 다음과 같다.
#include <iostream>
#include <vector>
#include <algorithm>
#include <string>
#include <string.h>
#include <stack>
#include <cmath>
#include <queue>
#include <numeric>
#include <tuple>
#include <map>
#include <set>
using namespace std;
int T, W;
int drops[1009];
int dp[1009][39];
int ret;
int go(int time, int moveCnt)
{
if (time > T || moveCnt > W) return 0;
if (dp[time][moveCnt] != -1) return dp[time][moveCnt];
int pos = moveCnt % 2 == 0 ? 1 : 2;
int isCatched = drops[time] == pos ? 1 : 0;
dp[time][moveCnt] = max(go(time + 1, moveCnt), go(time + 1, moveCnt + 1)) + isCatched;
return dp[time][moveCnt];
}
int main()
{
memset(dp, -1, sizeof(dp));
cin >> T >> W;
for (int t = 1; t <= T; ++t)
{
cin >> drops[t];
}
ret = max(go(1, 0), go(1, 1));
cout << ret << "\n";
return 0;
}